Parallelogram of Forces:
If a material point is acted upon by two forces represented by straight lines,
both in magnitude and direction, the resultant will be exactly represented by the
diagonal of the parallelogram of which the two lines are sides.
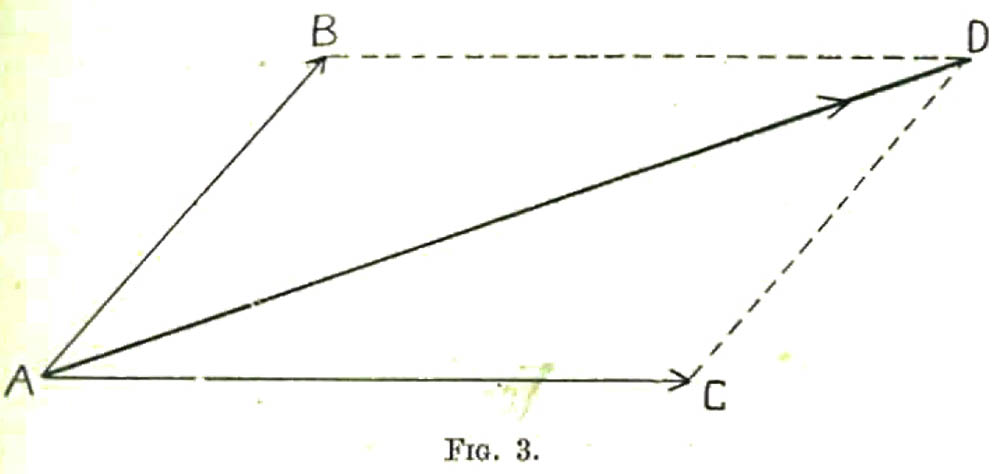
Two forces acting upon point A
Let A B and AC be the two forces, acting upon point A.
Their combined action will be represented in direction by the direction of the diagonal AD, and in
intensity[1] by the length of this diagonal.
Composition of Co-planar Forces:
The principle of the parallelogram of forces may be applied to the composition of any number of co-planar forces,
by taking each two forces in turn and finding their resultant, which is then combined with one of the remaining
forces to find a further partial resultant [2]. .
When the last partial resultant has been combined on the parallelogram principle with the last single force,
the resulting diagonal will be the total resultant of all forces.
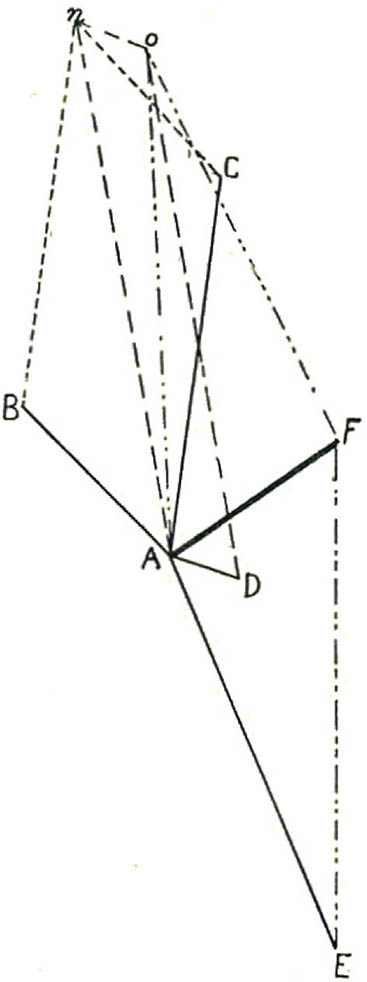
Let A be a point acted upon by four forces in one plane, their magnitudes and directions being represented by the lines AB, AC, AD, and AE respectively. The partial resultant of the forces AB and AC will be An ; that of the forces An and AD will be Ao.
Finally, that of the forces Ao and A E will be AF. The total result of the action of the four original forces
And a single force of this magnitude and direction acting upon A would produce exactly the same effect upon A as the combined action of the four given forces.
Finally, that of the forces Ao and A E will be AF. The total result of the action of the four original forces
- AB,
- AC,
- AD, and
- AE
And a single force of this magnitude and direction acting upon A would produce exactly the same effect upon A as the combined action of the four given forces.
[1]intensity: Within the context of vector analysis, intensity means force.
[2]partial resultant: The parallelogram law, and this partial resultant can then be combined with F, in a similar manner to find the resultant of all three forces.
Physics Problem Solver