Measuring Force in Piano Technique
A force may be measured by the work it does, which in turn is shown in the time and distance through which an object is moved.
Assuming that
At the end of 5 seconds, therefore, the arm will have covered a distance of 30 inches.
Now suppose that a force of 1 acts during the first second.
This will move the arm through 1 inch (5 inches less than the distance before).
Then a force of 3.5 will move it 3.5 inches during the 2nd second, giving a total displacement of 4.5 inches in two seconds.
At a similar rate of increase of force, the arm will move
The straight line shows the arm-displacements when the maximum velocity is attained at the beginning and maintained throughout the stroke. The upper, curved line shows the displacements with a slow beginning and increase of velocity during the movement. The dark points show the positions of the moving body at each second.
- inertia,
- atmospheric and joint resistances,
- and gravity
At the end of 5 seconds, therefore, the arm will have covered a distance of 30 inches.
Now suppose that a force of 1 acts during the first second.
This will move the arm through 1 inch (5 inches less than the distance before).
Then a force of 3.5 will move it 3.5 inches during the 2nd second, giving a total displacement of 4.5 inches in two seconds.
At a similar rate of increase of force, the arm will move
- 6 inches during the third second (or a total of 10.5 inches) ;
- 8.5 in the fourth;
- 11.0 in the fifth.
The straight line shows the arm-displacements when the maximum velocity is attained at the beginning and maintained throughout the stroke. The upper, curved line shows the displacements with a slow beginning and increase of velocity during the movement. The dark points show the positions of the moving body at each second.
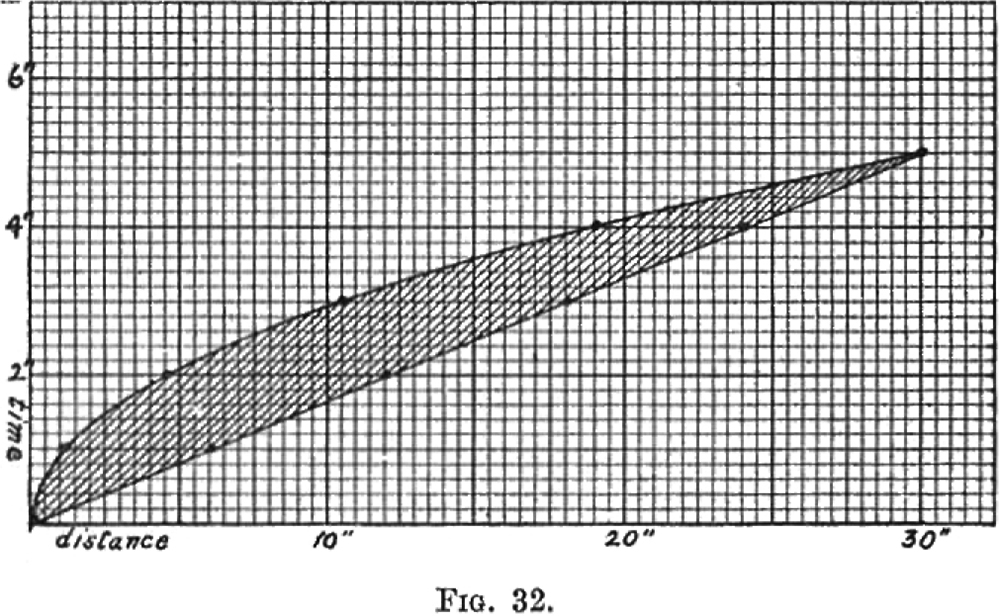
Description of Figure 32
Finally, the shaded portion may serve to indicate the excess energy required in giving to the arm its necessary final velocity
after a slow beginning. The figure is purely diagrammatic. Records of actual movements are given later.
Thus, by using a maximum at the beginning of the movement, a force of six suffices.
By beginning slowly and adding force throughout the movement, a final maximum force of eleven is needed, almost double the other. Various rates of increase are possible, but regardless of the actual rate, any increase during the movement represents excess energy. Which, as we have seen is characteristic of in-coordinated, not coordinated movements.
Thus, by using a maximum at the beginning of the movement, a force of six suffices.
By beginning slowly and adding force throughout the movement, a final maximum force of eleven is needed, almost double the other. Various rates of increase are possible, but regardless of the actual rate, any increase during the movement represents excess energy. Which, as we have seen is characteristic of in-coordinated, not coordinated movements.
But it does not follow that this advantage applies to slow movements. The slower the movement the greater is the effect of the
constant factors, previously ignored:
Again, assume the joint-resistance through the 30 inches of movement to be 60, the mass of the arm 10, and its acceleration 6.
- atmospheric and joint resistances,
- gravity, and
- inertia.
Again, assume the joint-resistance through the 30 inches of movement to be 60, the mass of the arm 10, and its acceleration 6.
F=ma (Newton's second Law)
Since force equals the product of the mass and the acceleration, the force of the moving arm will be (10 X 6) = 60, sufficient to overcome the joint-resistance. Now suppose the speed of the same arm to be 2 instead of 6. Its force will then be 10 x 2 or 20, only one-third of the force necessary to overcome the resistance. At the same time gravity acts for a longer period and its force is correspondingly increased. Gravity itself, still remains a constant, but the length of time during which it acts increases its force-effect.
Implement Continuous Motions, Avoid Discontinuous Motions
The alternative would be a jerky movement, in which the arm would move in spurts, resting between them.
Such a movement is so obviously at a mechanical and physiological disadvantage that we can at once exclude it from consideration.
In recording slow movements, therefore, we may expect to find a less intense but more prolonged muscular contraction than in
rapid movements. As the speed of movement increases, the initial muscular contraction should become more and more
noticeable.